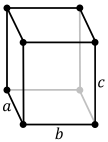
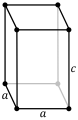
File:Triclinic.svg
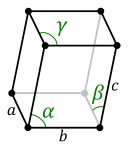
+ + +
Original file (SVG file, nominally 129 × 149 pixels, file size: 16 KB) +
File history
+Click on a date/time to view the file as it appeared at that time. +
+| Date/Time | Thumbnail | Dimensions | User | Comment | |
|---|---|---|---|---|---|
| current | 09:32, 8 August 2016 |  | 129 × 149 (16 KB) | Officer781 | Remove incorrect lattice constraint. The triclinic lattice has no constraints since it is the general case. One angle can be 90 degrees and it will still be triclinic. |
| 11:39, 31 July 2016 |  | 129 × 165 (26 KB) | Officer781 | Labelled a, b and c. | |
| 19:53, 21 May 2012 |  | 129 × 154 (26 KB) | Tretyak | Сorrection of an error | |
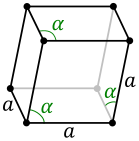
| 21:44, 2 March 2007 |  | 129 × 154 (25 KB) | Stannered | {{Information |Description=Triclinic crystal structure. |Source=Crystal stucture |Date=2007-03-02 |Author=Original PNGs by Daniel Mayer, traced in Inkscape by User:Stannered |Permission=GNU Free Documentation License |other_versio |
File usage
+-
+
- Bravais lattice +
- Crystal structure +
- Crystal system +
- Crystallographic point group +
- Cubic crystal system +
- Hexagonal crystal family +
- Hexagonal lattice +
- Lattice (group) +
- List of space groups +
- Monoclinic crystal system +
- Oblique lattice +
- Orthorhombic crystal system +
- Rectangular lattice +
- Space group +
- Square lattice +
- Tetragonal crystal system +
- Triclinic crystal system +
- Unit cell +
- User:Blo067~enwiki +
- User:DrBob/Figures +
- User:JTiago/Sandbox +
- User:Kazkaskazkasako/Books/Physical sciences +
- User:Tomruen/Space groups +
- Template:Crystal systems +
- Template:Infobox element/crystal structure +
- Template:Infobox element/crystal structure/doc +
Global file usage
+The following other wikis use this file: +
-
+
- Usage on af.wikipedia.org + +
- Usage on ar.wikipedia.org
+
- بنية بلورية +
- نظام بلوري +
- شبكة برافيه +
- وحدة الخلية +
+ - Usage on ast.wikipedia.org + +
- Usage on be.wikipedia.org + +
- Usage on bg.wikipedia.org + +
- Usage on bh.wikipedia.org + +
- Usage on bs.wikipedia.org + +
- Usage on ca.wikipedia.org + +
- Usage on ceb.wikipedia.org + +
- Usage on cs.wikipedia.org + +
- Usage on cy.wikipedia.org + +
- Usage on da.wikipedia.org + +
- Usage on de.wikipedia.org + +
- Usage on de.wikibooks.org + +
- Usage on el.wikipedia.org + +
- Usage on en.wikibooks.org + +
- Usage on en.wikiversity.org + +
View more global usage of this file. +
 +
+